양의 정부호 행렬

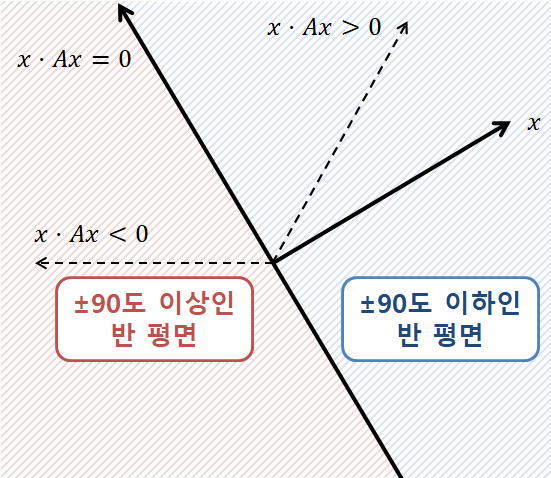
• 벡터의 선형변환시 +-90도 이하인 평면에 위치시키는것을 양의 정부호 행렬이라고 한다.

• 선형변환후 다시 x를 내적해주었을때 양수가 나와야한다.

양의 정부호와 고유값

• $Ax=\lambda x$

• $x^TAx = x^T\lambda x=\lambda

  x

  ^2$

$x^TAx$>0 고유값과 고유벡터 정의에 의해 양수이다 그러므로 $\lambda>0$ 즉 양의 정부호 대칭행렬이면 고유값들은 0이상의 실수 고유값들을 가진다!?

라플라시안 행렬

• 여기서 e는 1로이루어진 열벡터(라플라시안 그래프특성상 0나옴)
• 양의정부호 행렬 조건만족으로 모든 고유값은 0이상의 실수고유값 가짐
• 라플라시안 행렬은 준양의정부호 행렬임